XII. CREATION OF AMBIENT AIR POLLUTION MAPS
Directive No. 2008/50/EC on ambient air quality and on cleaner air for Europe, which is implemented into the Czech legislation (i.a. Decree No. 330/2012 Coll.), requires that the air quality be evaluated in all the zones and agglomerations of each member state. It further requires that the primary source of the evaluation be the results of stationary measurements. In the creation of air pollution maps, the measured concentrations may be supplemented by modelling and indicative measurements, so that the resultant estimate provides sufficient information on the spatial distribution of the pollutant concentrations in the air. The requirement to use stationary measurements as primary sources of information is related especially to areas in which the pollutant concentrations exceed the upper assessment threshold. This requirement is applied for the whole territory of the Czech Republic to ensure uniformity of the map creation methodology.
The basic source of data for creating air pollution maps thus consists in the pollutant concentrations measured at the individual monitoring stations. There are only a limited number of monitoring stations. In addition to the measured (primary) data, creation of maps is also based on the use of various supplementary (secondary) data, which provide comprehensive information about the entire territory and simultaneously exhibit regression dependence on the measured data. The main secondary source of information consists in models of pollution transport and dispersion, based on data from emission inventories and meteorological data. In the Czech Republic, mainly the Eulerian chemical dispersion model CAMx is used, supplemented by the SYMOS Gaussian model and the European EMEP Eulerian model. In addition, for individual pollutants, data are used on the altitude and population density (see Annex I fCombination of primary and secondary data is based on both the precision of the primary measured data and complete coverage of the whole territory by the secondary data. In regular map creation for the yearbook, the linear regression model is used with subsequent interpolation of its residuals. The kriging and IDW models are used as interpolation methods (see Annex I for details).
Urban and rural air pollution have different character; in general, urban pollution is affected by emissions and is generally higher than rural air pollution. However, air pollution by tropospheric ozone, where conditions are the opposite, is an exception. Thus urban and rural maps are created independently and the resultant map is a product of combination of the urban and rural maps using the grid of population density. For a number of pollutants (see Annex I), the traffic layer is considered in addition to the urban and rural layers. This layer is merged with the urban and rural background layers using the grid of traffic emissions. The measured air pollution data from the background rural stations are used as primary data for construction of rural maps. Air pollution data from urban and suburban background stations are used for urban maps. Data from traffic stations are used for the traffic layers. Simultaneously, the individual stations are classified according to the AQIS database.
The maps are created using geographic information systems (GIS). The main data source is the AQIS relational database of measured emissions and the chemical composition of atmospheric precipitation. The maps are constructed with spatial resolution of 1 x 1 km, in the Gauss-Krüger projection. Annex I gives detailed specification of mapping for the individual pollutants.
Since 1994, the digital DMÚ 200, DMR-2, DMÚ25 and later the ZABAGED layers have been used as a foundation for the basic geographic and thematic layers in the standard projection (Gauss-Krüger conformal projection). In recent years, the basic information provided by CSO has been used for updated layers of administrative classification.
Mapping of rural and urban (and potential traffic) layers
Maps of rural and urban background pollution (and, where applicable, also traffic pollution) are prepared separately, constructed on the basis of combinations of primary (measured) and secondary (model and other supplementary) data (Horálek et al. 2007) The methodology employed consists in the linear regression model with spatial interpolation of its residuals. This methodology enables the use of supplementary data for the entire mapped territory. Where there are no suitable supplementary data, simple interpolation of the measured data is employed. The estimate is calculated using the relationship:
![]() (1)
(1)
where
![]() is the estimated value of the concentration in the point s0,
is the estimated value of the concentration in the point s0,
Xi(s)
are various supplementary parameters in the point s0 for
i = 1, 2, …p,
c, a1, a2,… are
the parameters of the linear regression model,
h(s0)
is the spatial interpolated value of the residuals of the linear
regression model in the point s0,
calculated on the basis of the residuals in the points of
measurement.
The interpolation is performed either using the inverse distance weighting method (IDW) or using the ordinary kriging (specification for individual pollutants is given in Annex I). The IDW method is a simple deterministic method, where the weight of the individual measuring stations in the interpolation depends only on their distance from the estimated point. On the other hand, kriging is a more advanced geostatistical method taking into account the structure of the air pollution field. However, the IDW method has the advantage that this interpolation respects the measured values in the points of the measuring stations. Kriging does not, in general, respect the measured values. A solution lies in interpolation using kriging and applying IDW to its residuals at the measuring sites.
Interpolation of residuals using IDW is calculated according to the relation:
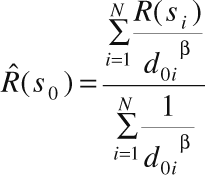 (2)
(2)
where
![]() is the estimate of the field of residuals in the point s0,
is the estimate of the field of residuals in the point s0,
R(si)
is the residual of linear regression model in the point of
measurement si,
N
is the number of surrounding stations used in interpolation,
d0i
is the distance between points s0
and si,
b
is
the weight.
In ordinary kriging the interpolation of residuals is
calculated according to the relation:
![]() při
při
![]() (3)
(3)
where
l1,
…,lN
are the weights estimated on the basis of fitted variogram (see
below),
R(si)
is the residual of linear regression model in the point of
measurement si.
The variogram describes the dependence of the between-points
variability on the mutual distance of points, it is a measure of
a spatial correlation (see e.g. Cressie 1993). The variogram is
estimated by fitting spherical function in empirical variogram,
calculated according to the relation:
where
![]() is the empirical variogram of the field of residuals,
is the empirical variogram of the field of residuals,
R(si), R(sj) are
the residuals in the points of measurement si and
sj,
dij
is the distance of points si
and sj,
n
is the number of station couples si and sj,
with their mutual distance h±d,
d is
the tolerance.
Spherical function and variogram parameters range, nugget and
sill are illustrated in
Fig. XII.1.
The calculated urban and rural (and potential traffic) layers
are subsequently merged.
Merging of urban and rural
(and, as appropriate, traffic) layers
The population density layer is used for merging
the urban and rural layers (Horálek et al. 2007;
De Smet et al. 2011). Merging is carried out using
the relationship
![]() for
for
![]()
![]() for
for
![]() (5)
(5)
![]() for
for
![]()
where
![]() is the result estimate of the concentration in the point s0,
is the result estimate of the concentration in the point s0,
![]() is
the concentration in the point s0 for the rural or
urban map,
is
the concentration in the point s0 for the rural or
urban map,
a(s0)
is the population density in the point s0,
a1,
a2
are classification intervals of the respective population
density (see the Annex I).
The entire concept of separate mapping of rural and
urban pollution is based on the assumption that
![]() for all common pollutants with the exception of ozone, or
for all common pollutants with the exception of ozone, or
![]() or ozone. For areas
where this assumption is not fulfilled, a layer created
similarly to the urban and rural layers is used; nonetheless, it is created on the basis of all the background
stations without distinguishing between
urban and rural stations.
or ozone. For areas
where this assumption is not fulfilled, a layer created
similarly to the urban and rural layers is used; nonetheless, it is created on the basis of all the background
stations without distinguishing between
urban and rural stations.
If traffic pollution is also mapped for the relevant
pollutant, the traffic layer is added to the background
(merged urban and rural) layer using the
grid of traffic emissions:
![]() for
for
![]()
![]() for
for
![]() (6)
(6)
![]() for
for
![]()
where
![]() is the result estimate of the concentration in the point s0,
is the result estimate of the concentration in the point s0,
![]() is the concentration in the point s0 for the
background layer,
is the concentration in the point s0 for the
background layer,
![]() is the concentration in the point s0 for the traffic
layer,
is the concentration in the point s0 for the traffic
layer,
t(s0)
are traffic emissions in the point s0,
t1,
t2
are the classification intervals of the respective traffic emissions (see the Annex I).
The above function is based on the assumption that
![]() for common pollutants, except ozone, where
for common pollutants, except ozone, where
![]() for ozone. The background
layera
for ozone. The background
layera
![]() is used for areas where this assumption
is not fulfilled.
is used for areas where this assumption
is not fulfilled.

Fig. XII.1 Diagram showing the variogram parameters and the
fitted spherical functions